2014江苏公务员考试资料分析技巧-增长率相关速算法
提示
使用“差分法”的时候,牢记将“差分数”写在“大分数”的一侧,因为它代替的是“大分数”,然后再跟“小分数”做比较。
两年混合增长率公式:
如果第二期与第三期增长率分别为r1与r2,那么第三期相对于第一期的增长率为:r1+r2+r1×r2
增长率化除为乘近似公式:
如果第二期的值为A,增长率为r,则第一期的值A’:A’=≈A×(1-r)
(实际上左式略大于右式,r越小,则误差越小,误差量级为r2)
减少率化除为乘近似公式:
如果第二期的值为A,减少率为r,则第一期的值A’:A’=≈A×(1+r)
(实际上左式略大于右式,r越小,则误差越小,误差量级为r2)
平均增长率近似公式:
如果N年间的增长率分别为r1、r2、r3……rn,则平均增长率:r≈
(实际上左式略小于右式,增长率越接近,误差越小)
求平均增长率时特别注意问题的表述方式,例如:
1、“从2004年到2007年的平均增长率”一般表示不包括2004年的增长率;
2、“2004、2005、2006、2007年的平均增长率”一般表示包括2004年的增长率。
“分子分母同时扩大/缩小型分数”变化趋势判定:
1、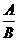 中若A与B同时扩大,则①若A增长率大,则
中若A与B同时扩大,则①若A增长率大,则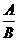 扩大②若B增长率大,则
扩大②若B增长率大,则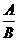 缩小;
缩小;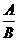 中若A与B同时缩小,则①若A减少得快,则
中若A与B同时缩小,则①若A减少得快,则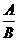 缩小②若B减少得快,则
缩小②若B减少得快,则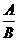 扩大。
扩大。
1、“从2004年到2007年的平均增长率”一般表示不包括2004年的增长率;
2、“2004、2005、2006、2007年的平均增长率”一般表示包括2004年的增长率。
“分子分母同时扩大/缩小型分数”变化趋势判定:
1、
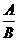 中若A与B同时扩大,则①若A增长率大,则
中若A与B同时扩大,则①若A增长率大,则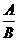 扩大②若B增长率大,则
扩大②若B增长率大,则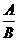 缩小;
缩小;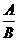 中若A与B同时缩小,则①若A减少得快,则
中若A与B同时缩小,则①若A减少得快,则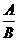 缩小②若B减少得快,则
缩小②若B减少得快,则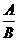 扩大。
扩大。
2、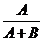 中若A与B同时扩大,则①若A增长率大,则
中若A与B同时扩大,则①若A增长率大,则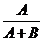 扩大②若B增长率大,则
扩大②若B增长率大,则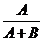 缩小;
缩小;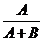 中若A与B同时缩小,则①若A减少得快,则
中若A与B同时缩小,则①若A减少得快,则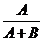 缩小②若B减少得快,则
缩小②若B减少得快,则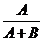 扩大。
扩大。
多部分平均增长率:
如果量A与量B构成总量“A+B”,量A增长率为a,量B增长率为b,量“A+B”的增长率为r,则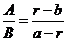 ,一般用“十字交叉法”来简单计算:
,一般用“十字交叉法”来简单计算:
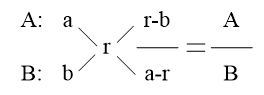
注意几点问题:
1、 r一定是介于a、b之间的,“十字交叉”相减的时候,一个r在前,另一个r在后;
2、 算出来的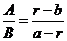 是未增长之前的比例,如果要计算增长之后的比例,应该在这个比例上再乘以各自的增长率,即
是未增长之前的比例,如果要计算增长之后的比例,应该在这个比例上再乘以各自的增长率,即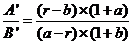 。
。
等速率增长结论:
如果某一个量按照一个固定的速率增长,那么其增长量将越来越大,并且这个量的数值成“等比数列”,中间一项的平方等于两边两项的乘积。
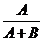 中若A与B同时扩大,则①若A增长率大,则
中若A与B同时扩大,则①若A增长率大,则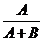 扩大②若B增长率大,则
扩大②若B增长率大,则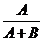 缩小;
缩小;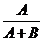 中若A与B同时缩小,则①若A减少得快,则
中若A与B同时缩小,则①若A减少得快,则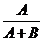 缩小②若B减少得快,则
缩小②若B减少得快,则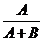 扩大。
扩大。多部分平均增长率:
如果量A与量B构成总量“A+B”,量A增长率为a,量B增长率为b,量“A+B”的增长率为r,则
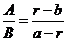 ,一般用“十字交叉法”来简单计算:
,一般用“十字交叉法”来简单计算:
注意几点问题:
1、 r一定是介于a、b之间的,“十字交叉”相减的时候,一个r在前,另一个r在后;
2、 算出来的
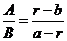 是未增长之前的比例,如果要计算增长之后的比例,应该在这个比例上再乘以各自的增长率,即
是未增长之前的比例,如果要计算增长之后的比例,应该在这个比例上再乘以各自的增长率,即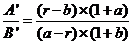 。
。等速率增长结论:
如果某一个量按照一个固定的速率增长,那么其增长量将越来越大,并且这个量的数值成“等比数列”,中间一项的平方等于两边两项的乘积。
 相关文章
相关文章





